統計学が苦手な療法士は多いように思います。そういう人のために「脱・統計学苦手療法士ロードマップを作成しました。
達成目標は「統計学の基礎的な知識を身につけて臨床に還元すること」です！
目次
理学療法士が統計学を学ぶメリット
統計学を学ぶとメリットがいっぱいあります。患者さんに検査・測定を行ってデータを扱う職種なので誤った解釈をしないためにも学んだほうが良いと思います。臨床だけではなく私生活にも使えますしね。学ばないとできないからこそ職場では重宝されますよ！
メリットを挙げると以下の通りになります。
- 検査・測定で得られた情報を正しく解釈できる
- 論文を解釈できるようになる
- 変な情報に騙されないようになる
- 研究をしようと思ったときに使用できる
理学療法士が統計学を学ぶメリット
統計学とは
「そもそも統計学とはなんぞや？」と思うことがあると思います。
統計学は厳密さを恐れずに言うと
「データをどのように分析し、どのような判断をくだしたら良いのか？」を論ずる学問であり、
「データの背景にある現象の法則性を知るための学問」です。
全体を入念に調べて全体の法則性を見出すことや、全体の中の一部を知ることで論理性のある推論から全体の法則性を導く手段です。
統計学の概要
変数の分類
理学療法現場で得られる検査や計測などで得られたデータは性質によって4つに分けることができます。
変数の性質を知ることによって、誤った数値の扱いを避けることができます！！
変数の分類をまとめると以下の通りです。
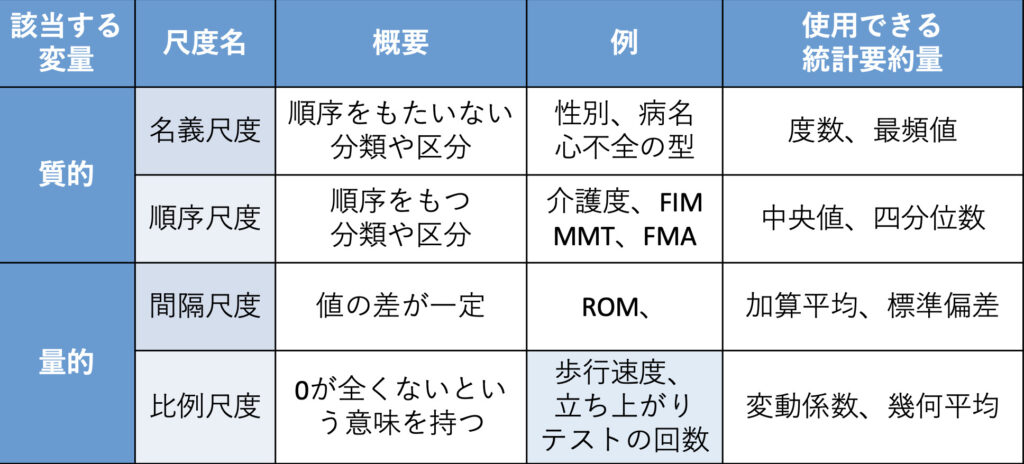
変数の分類
母集団と標本
統計学的に物事を考えるときに意識してほしいことの1つに「母集団がどの範囲なのか？」ということがあります。
母集団と標本を一言で言うと
母集団（population）は「実験や調査の対象となる集まり」です。
標本（sample）は「ある母集団から抽出した個体の集まり」です。
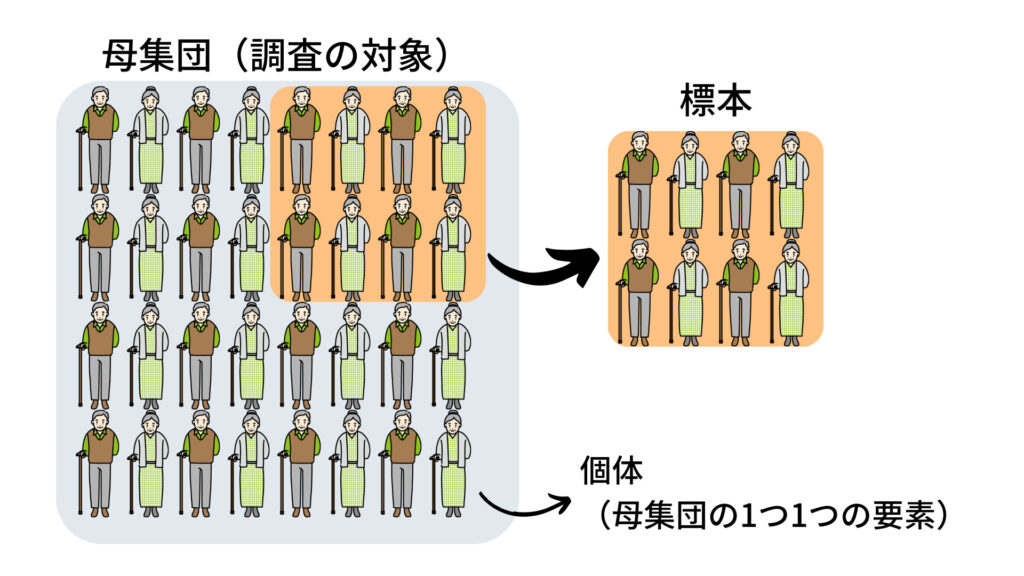
母集団と標本
誤差について
観測された結果には必ず誤差が含まれています。誤差の種類は大きく2つに分けることができます。
「偶然誤差」と「系統誤差」です。この2つを一言で表すと
- 偶然誤差は「ばらつき」
- 系統誤差は「偏り」
となります。
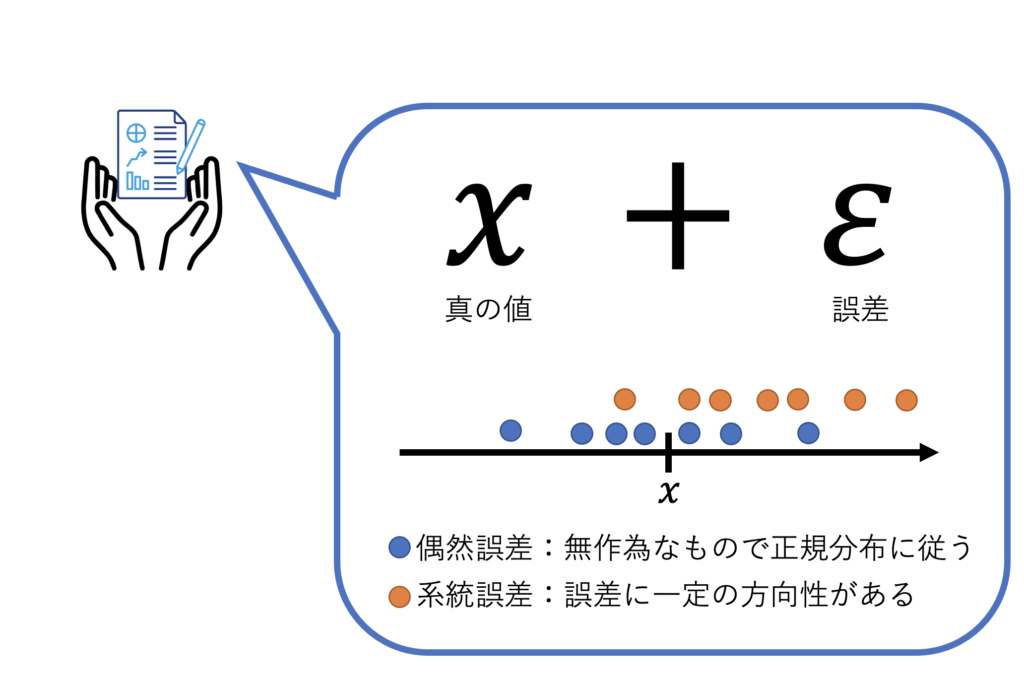
誤差について
度数分布とヒストグラム
度数分布表とは観測値の取りうる値をいくつかの階級（値の範囲）に分けて、その階級内に観測値がいくつあるのか（度数）を表にしたもので、それを可視化したものがヒストグラムです。
度数分布やヒストグラムを使用すると1次元のデータの分布を簡単に把握することができます。
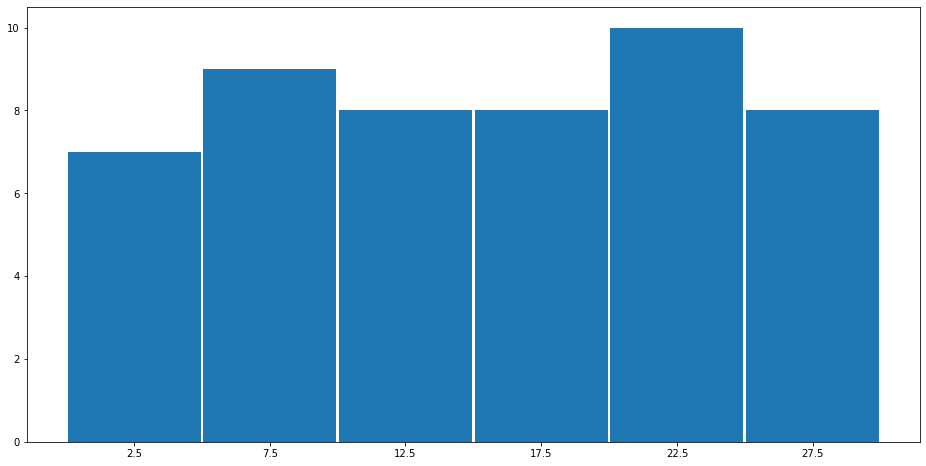
度数分布とヒストグラム
パーセンタイルと箱ひげ図
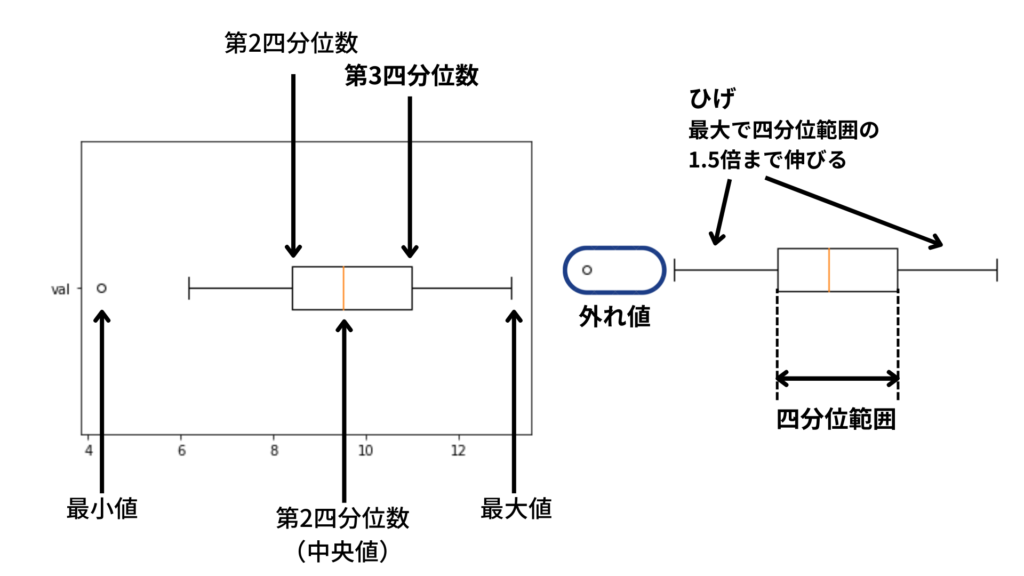
1次元のデータの可視化方法の1つに箱ひげ図があります。箱ひげ図は５要約数を可視化したもので、いいところは外れ値がわかりやすいところです。
ちなみに5要約数はパーセンタイル（データを小さい順番に並べてどこに位置する値）の特殊な場合です。
| パーセンタイル | 要約数 |
| 0％ | 最小値 |
| 25％ | 第1四分位数 |
| 50％ | 第2四分位数（中央値） |
| 75％ | 第3四分位数 |
| 100％ | 最大値 |
パーセンタイルと箱ひげ図
分布の特徴を表す指標
分布を特徴を表す指標がいくつかあります。これらの指標はある値で表すことができるので、視覚的に判断する「ヒストグラム」や「箱ひげ」よりも客観的に判断することができます。
パーセンタイルを使って算出する中央値や範囲も分布の特徴を表す指標ですね！
そのほかには平均値、分散、標準偏差などがあります。
平均値は分布の中心の指標であり、分散や標準偏差は分布のばらつきの指標になります。
分布の特徴を表す指標
2変数の関係性（量的データ）
2つの変数間の互いの関係で特に2つの変数間に区別を設けずに対等にある関係を相関（correlation）と言います。
一方で変数aから変数bを推定したい！という関係性を回帰（regression）と言います。
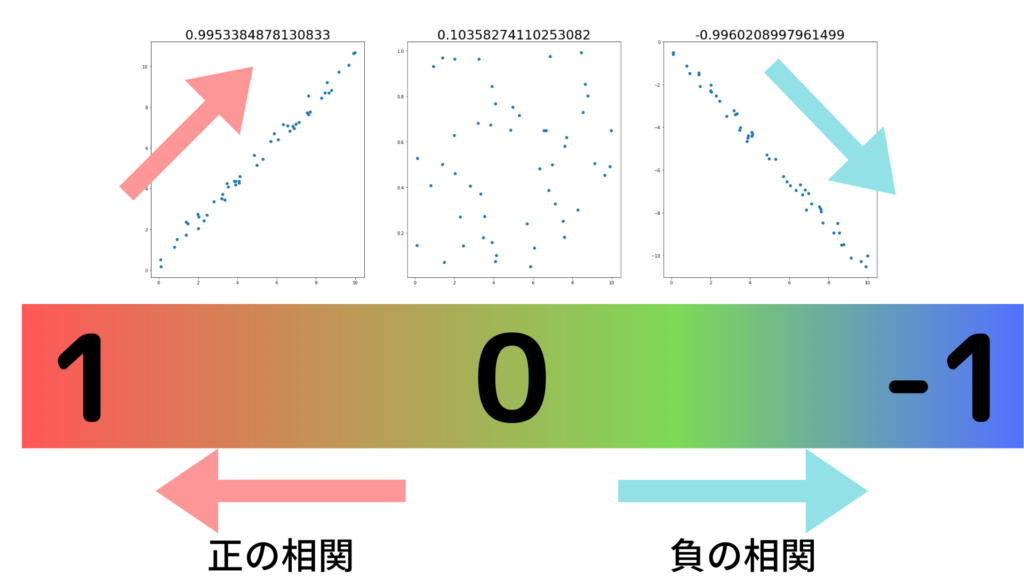
2変数間の関係を図で表したものを散布図、散布図の直線関係を数値化したものが相関係数です。特に関係性を知りたい2変数が量的データである場合はピアソンの積率相関係数を用います。
2変数の関係性（量的データ）
2変数の関係性（質的データ）
関係性を知りたい2変数がどちらも質的データであれば散布図を用いて可視化やピアソンの積率相関係数を使って直線関係を知ることができましたが、質的なデータになるとこれらの手法は使いにくいです。
そんな時に便利なのがクロス集計表やヒートマップです
2変数の関係性（質的データ）
時系列データ
時系列データはある単位時間ごとに観測されたものです。ある単位時間ごとに計測をしているのでデータの順序が強い意味を持ちます。そのため、因果関係の解明や時間的な周期変動、予測などを知るために利用することができます。
時系列データ
統計学では手元にあるデータ（標本）からデータの元となっている母集団を推定する時には確率（probability）の考え方が大事になってきます。
というもの、起こりうる結果がどういう要素を含んでいることはわかりますが、1回ごとの結果は偶然に左右されて事前に予測することは困難です。
例を挙げると、
- サイコロを振る時に起きうる結果がどういう要素を含むかは事前にわかるが、次にふった時に出る目は偶然に左右される。
- ある介入Aを行うと、どの程度の治療結果をが得られたかは過去のデータからわかるが、目の前の人に介入Aを行った時に得られる治療結果は分からない。
- どのような人が転倒したのかは過去のデータからわかるが、目の前の人が明日転倒するかは分からない
といったようにこういった偶然に左右される不確実でランダムな問題と戦わなければならない。統計学においてこのランダム性と戦うツールが確率なのです。
統計学と確率
確率変数は様々な値をとりうる変数Xがあって、それぞれの値をとる確率が決まっているときXを確率変数といいます。また
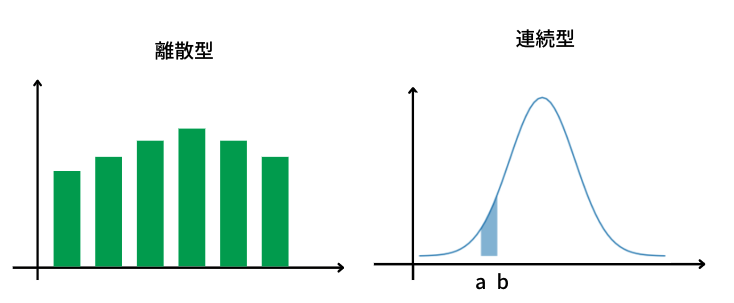
確率変数を一目でわかりやすく表したものです（図や表で表すことが多い）。表で表す場合は横軸に確率変数、縦軸に確率変数の起こりやすさを表した分布です。離散型の場合は一つの値に対応する縦軸が起こりやすさを表しますが、連続型の場合は面積が起こりやすさを表しています。
確率変数と確率分布
基本的にはこの本を読めば書いてありますが、少し読みにくいと感じる人もいると思います。
その他のオススメ書籍もあるので、参考にしてください。
