誤差について

サバくん

同じ人に同じ検査を同じ日に測っても数値が違うことがありますよね？

その原因は検査や測定を行なって手元にあるデータはには誤差が含まれているからです。

誤差

この記事にも書いたように

「データをどのように分析し、どのような判断をくだしたら良いのか？」や「データの背景にある現象の法則性」を知るためには事実を観測することが必要です

しかし、観測された結果には必ず誤差が含まれています。様々誤差がありますが、この記事を読むことで誤差についての知識が整理されます。

誤差の種類は大きく2つに分けることができます。「偶然誤差」と「系統誤差」です。この2つを一言で表すと

偶然誤差は「ばらつき」、系統誤差は「偏り」となります。では詳しく見ていきましょう。

偶然誤差（ramdom error）

偶然誤差は理想的な条件のもとで多くの測定を繰り返したときに偶然生じるものでばらつきのことです。偶然誤差を手元のデータから取り除くことは困難です。

偶然誤差には測定のときに生じる測定誤差や個体差などがあります。基本的にばらつきは正規分布と呼ばれる誤差の分布に従うことが多いです。

系統誤差（systematic bias）

系統誤差はデータの収集方法が適切でないため起こる一定の傾向を持つデータの偏りです。

この偏りは事実を歪めるため、良いものではありません。なのでできるだけ取り除くようにしなければなりません。

系統誤差には2つの種類があります。「固定誤差」と「比例誤差」です。

固定誤差（fixed bias）は真の値の大小に関わらず、特定の方向に生じる誤差のことです。

比例誤差（proportional bias）は真の値の大きさに比例して大きくなる誤差のことです。

まとめ

この記事をまとめたものが以下の図になります。

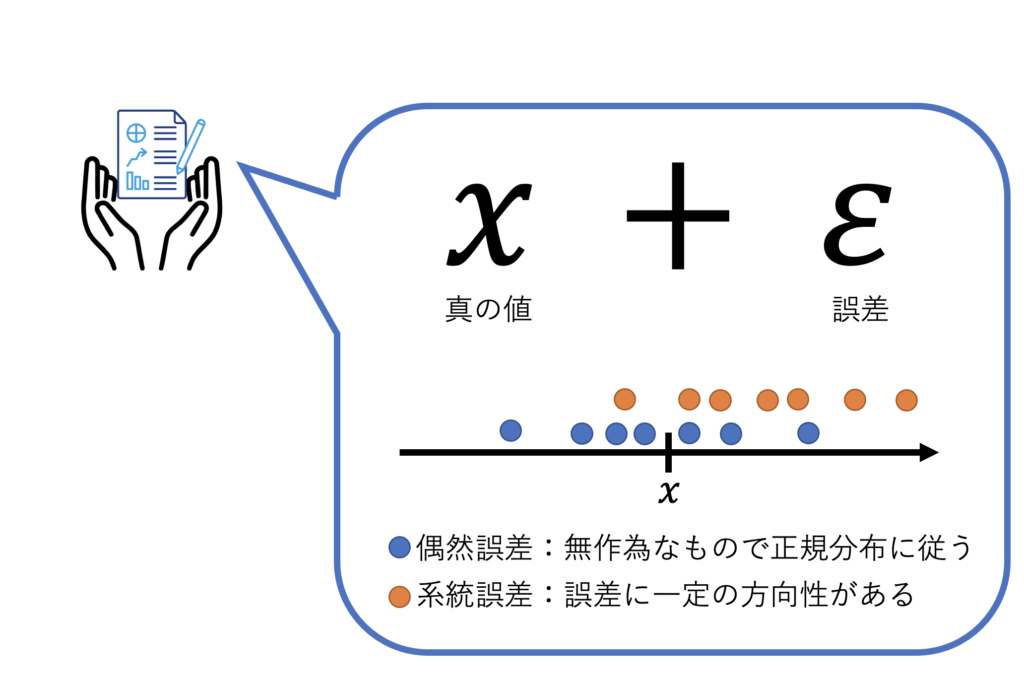
個体における手元にあるデータにはどの程度誤差が含まれているのかが判断できません。集団であれば、Bland-Altman plotという図を用いて分析を行うことで系統誤差の有無が確認できますが、その話はまた違う記事でお話しします。

脱・統計学苦手療法士ロードマップ