データを収集したり、何か疑問を解決したい時に変数間の関係を見たい時があると思います。
特に2つの変数の間にある関係性をみる時には散布図を使うとわかりやすいです。
目次
2つの変数間の互いの関係で特に2つの変数間に区別を設けずに対等にある関係を相関(correlation)と言います。
一方で変数aから変数bを推定したい!という関係性を回帰(regression)と言います。
具体例を挙げると
相関は関係の身長と体重のような対等な関係性です。どちらがどちらかを決めるわけではないので矢印は2方向性です。
身長⇆体重
回帰は 生理的断面積から筋力を推定したいといった関係です。この2群は生理的断面積→筋力と矢印が1方向となっています。
生理的断面積→筋力
例えば、10人の身長と体重を計測したとして以下の結果が得られたとします。
| 変数 | Aさん | Bさん | Cさん | Dさん | Eさん | Fさん | Gさん | Hさん | Iさん |
| 身長cm | 178 | 169 | 180 | 142 | 150 | 162 | 172 | 148 | 165 |
| 体重kg | 70 | 65 | 92 | 42 | 49 | 50 | 68 | 52 | 58 |
これらの結果を図にしてみましょう。縦軸に身長、横軸に体重をとってみましょう。
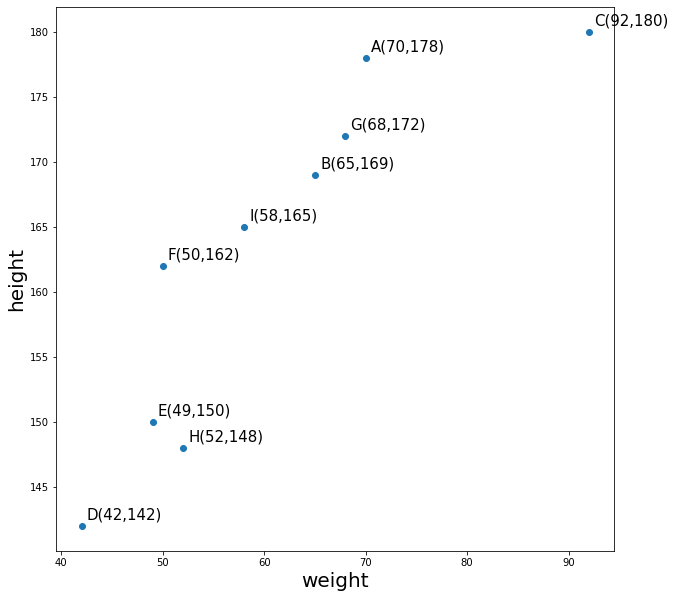
このような図を散布図と言います。表ではどのような2変数にどのような関係性があるのかわかりにくかったですが、散布図を図示することで2変数にどのような関係性(傾向)があるのかがわかりやすくなります。この散布図は2次元データの分析の最初に行われることが多いです。
統計学的に2変数の関係が直線関係に近い傾向ある時に強い相関があると表現します。逆に直線関係の程度が弱い場合は弱い相関がある、全く直線関係がない場合は無相関といった表現をします。
加えて、1変数が増加するともう一方も増加する場合は正の相関、もう一方が減少する場合は負の相関と言います。
この例では身長と体重という2変数の場合、身長が伸びると体重が増加することがわかります。つまり、強い正の相関がありそうです。
相関図を見て感覚的には2変数の関係性が掴めると思いますが、どの程度関係性があるのかを客観的にしたい場合があると思います。そんな時には相関係数(correlation coefficient)を用います。特に2変数がどちらも量的データであればピアソンの積立相関係数を使います。相関係数は−1〜1の値をとります。(ピアソンの積立相関係数の算出方法はまた別の記事にて、)
相関係数の解釈の仕方を図と表にすると以下の通りです。
| 相関係数の値 | 解釈 |
| 1に近い | 強い正の相関 |
| 0に近い | 無相関 |
| −1に近い | 強い負の相関 |
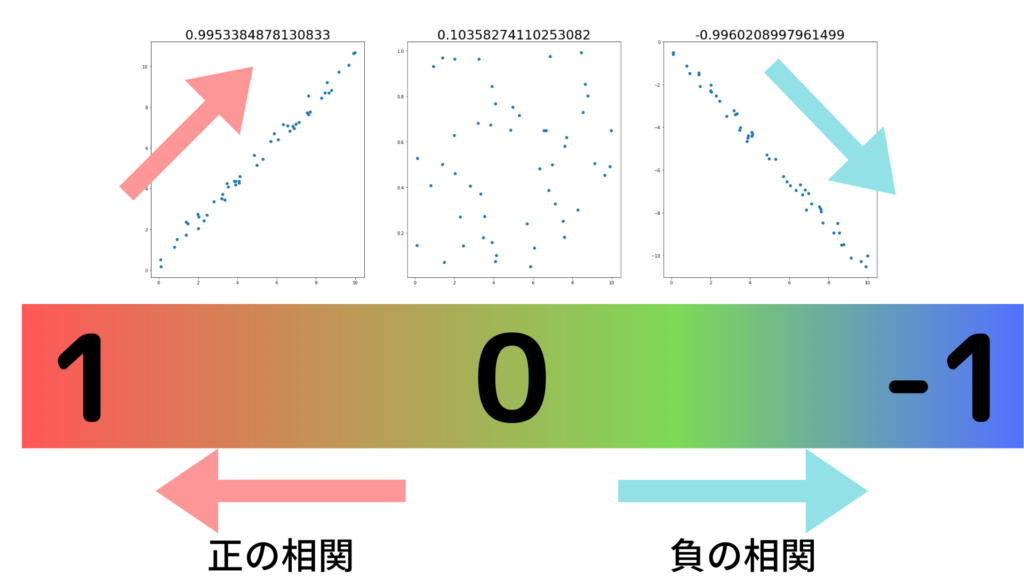
このように2変数の散布図をとった時の直線関係を定量化することで客観的に2変数の相関を判断することができます。