変数の分類

サバくん

検査や計測などで得られたデータは性質によって4つに分けることができます。変数の性質を知ることによって、誤った数値の扱いを避けることができます！！

量的データと質的データ

臨床で検査・測定を行うと手元にデータ（観測値）があると思いますが、そのデータは性質によって分けることができます。まず、大きく「質的データ」と「量的データ」の2つに分けることができます。

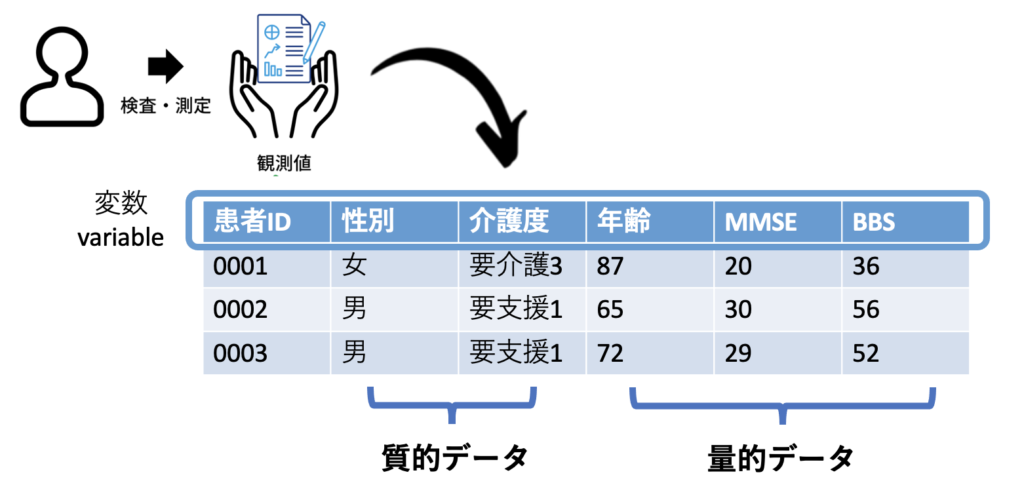
1つは量的データといい、もう1つは量的データといいます。

簡単に説明すると、量的データは観測値が属性や項目などのデータです。質的データは観測値が数値のデータです。詳しくみていきましょう。

質的データ（qualitative variable）

先に述べたように質的データは区分できるデータ、つまり属性や項目、区分や分類などのデータです。

リハビリ分野で言うと、性別や病名、心不全の型、介護度、MMTなどが挙げられます。

実はこの質的データはさらに2つの分類に分けることができます。どのような方法で分けるのかというと、「分類に順序があるのかどうかです。」

順序がないものは名義尺度、順序があるものは順序尺度と言います。

このような質的データを取り扱う場合に注意して欲しいことがあります。それは四則計算ができない点です。名義尺度であれば、「そんなこと当たり前じゃないか！！」と思うと思いますが、MMTやFIM、NRSのように順序を持った区分をリハビリテーション分野はよく使うので注意が必要です。

例を挙げると、

MMTが2から4に改善したからといって、筋力が2倍になったわけではないです。

また、MMTが2から4に改善したことと、MMTが3から5に変化した時、筋力が同程度向上したとは言えません。

このように質的データは四則計算が使えないので、使用できる統計要約量（集まったデータを表現する量）は限られます。

具体的に使用できる統計要約量は

名義尺度であれば、「度数」と「最頻値」

順序尺度であれば、「度数」と「最頻値」に加えて中央値、四分位数が使用できます。

サバくん

統計要約量については他の記事で記述します。

量的データ（quantitative variable）

次は量的データです。量的データは数値のデータです。

リハビリ分野で言うと、ROMや歩行速度、立ち上がりテストの回数などが挙げられます。

この量的データはさらに2つの分類に分けることができます。どのような方法で分けるのかというと、「0に全くないという意味があるのかどうかです。」他の言い方をすると「0が相対的なものなのか、絶対的なものなのか」ということです。

0に全くないという意味がないものは間隔尺度、0に全くないという意味があるものは比例尺度と言います。

このような量的データを扱うときの注意点は間隔尺度は0が相対的なものなので、数値が何倍になったという表現は適切ではありません。

例を挙げると

ある関節のROMが60度から120度に拡大したからといって、関節可動域は2倍にはなったとは言えません

使用できる統計要約量は

間隔尺度であれば、順序尺度で使用できる統計要約量に加えて、「加算平均」、「標準偏差」

比例尺度であれば、間隔尺度に使用できる統計要約量に加えて「変動係数」、「幾何平均」が使用できます。

離散変数と連続変数

ここでややこしいことを言います。実は量的データはもう1つの分け方があります。「離散的なのか、数値が連続的なのか」で分類できます。数式で表現するときに重要になってきます。ここでは「そんな分け方もあるのだなぁ」と思っていただければいいです。

まとめ

変数の分類について記述しました。この記事で説明したことをまとめると以下の表のようになります。

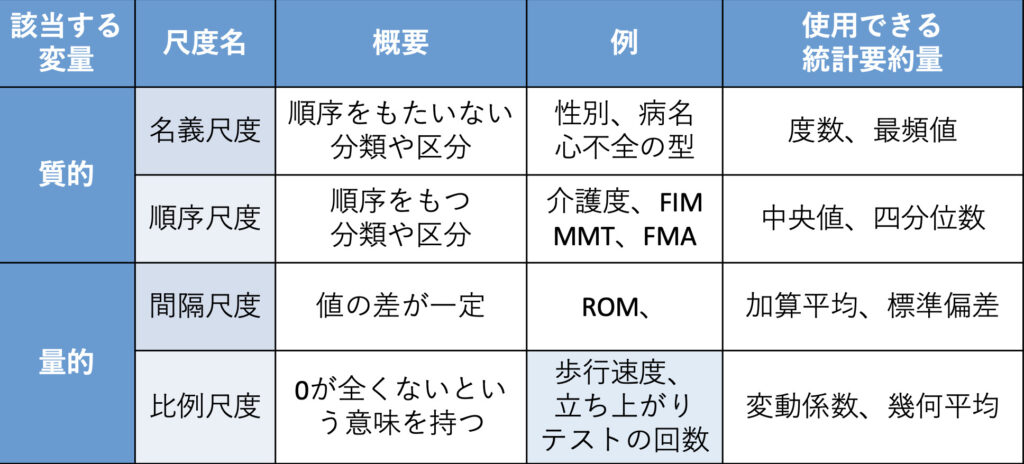
また、わかりにくいところや、もっと知りたいところがあればコメントよろしくお願いします。

脱・統計学苦手療法士ロードマップ