理学療法の分野では患者さんに定期的に検査・測定を行うことが多いと思います。
定期的に検査・測定した時に得られる時系列データについてみていきましょう。
目次
時系列データはある単位時間ごとに観測されたものです。ある単位時間ごとに計測をしているのでデータの順序が強い意味を持ちます。そのため、因果関係の解明や時間的な周期変動、予測などを知るために利用することができます。
実際に時系列データを見てみましょう！
ある人の血圧を毎日3時間10日間ごとに計測したとします。（ここでは簡単のために収縮期血圧のみにします）計測したデータを縦軸に血圧の値、横軸に時間をとったグラフを見てみます。
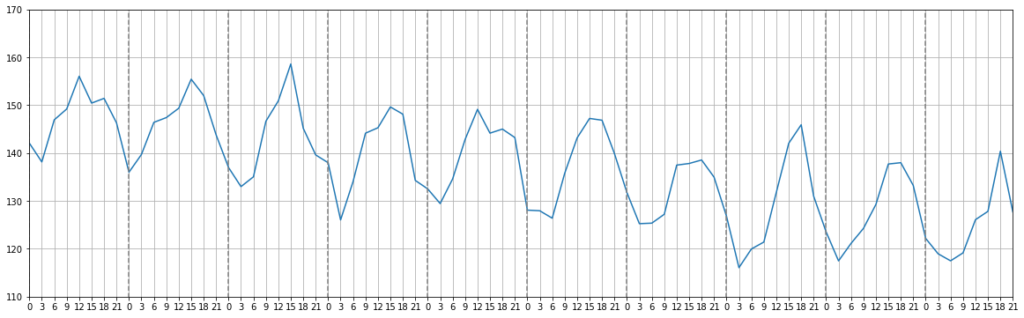
波打ちながら緩やかに減少していることが読み取れると思います。今回は3時間ごとに10日分のデータを計測しているので24÷3×10=80個のデータがあります。この80を時系列の長さと言います。
このような時系列データを把握するためには、長期にわたる変動である傾向と周期的な変動である周期を把握することがいいです。
傾向
血圧は日差変動があるのでこのようなデータになることが多いように思います。このような日差変動があると、長期にわたる変動が分かりにくいです。そんな時に便利なのが移動平均です。
移動平均は一定区間（窓幅）ごとの平均値を区間をずらしながら求める手法です。以下のグラフは窓幅を1（3時間）, 3（9時間）,7（21時間）とした時の移動平均の結果です。
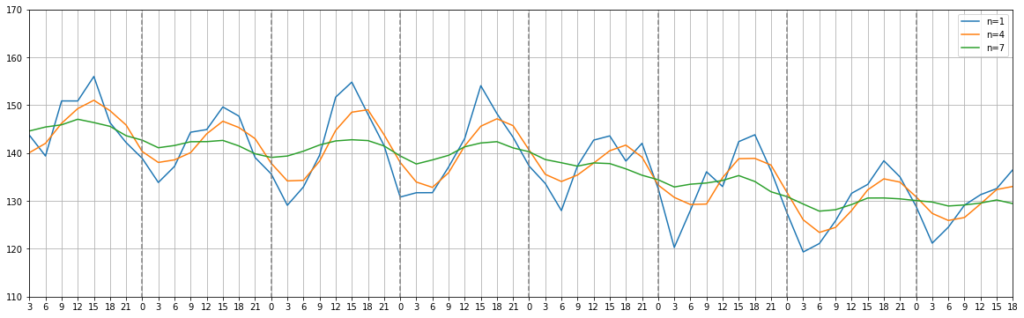
窓幅が大きいほど折れ線グラフが滑らかになり、傾向が掴みやすくなります。
移動平均の窓幅を大きくしすぎると意味のある変動も滑らかになってしまいます。窓幅の設定には注意が必要です。
周期
周期性を確認するためには自己相関係数（auto-correlation coefficient）を使用します。
ズレをh、配列をxとしたとき、ズレhの自己相関係数$r_h$は以下のように定義されます。
$$r_h=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(x_{i+h}-\bar{x})/(n-h)}{\sum_{i=1}^{n}(x_{i}-\bar{x})^2/(n)}$$
小難しい数式ですけど、簡単にいうとデータを一定数ずらして積率相関係数を求めます。
横軸にズレ、縦軸に相関係数をとったグラフ（コレログラフ）を見てみましょう。
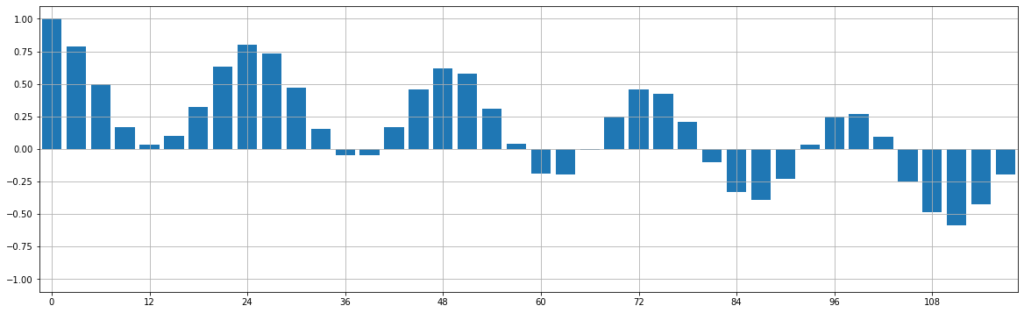
図を見ると、24の倍数で相関係数が高くなっていることがわかると思います。なので、今回得られた血圧のデータは24時間で周期的に変動していることがわかります。
時系列には他にも解析方法がたくさんあります。代表的なものであれば、周波数解析があります。
