
統計学的に物事を考えるときに意識してほしいことの1つに「母集団がどの範囲なのか?」ということがあります。
この記事では母集団に加えて、母集団と切っても切れない関係にある標本について記述します。
目次
まず、母集団と標本を一言で言うと
母集団(population)は「実験や調査の対象となる集まり」です。
標本(sample)は「ある母集団から抽出した個体の集まり」です。
標本を少しカタイ表現にすると「標本は母集団から抽出するごとに異なる値をとる確率変数」です。
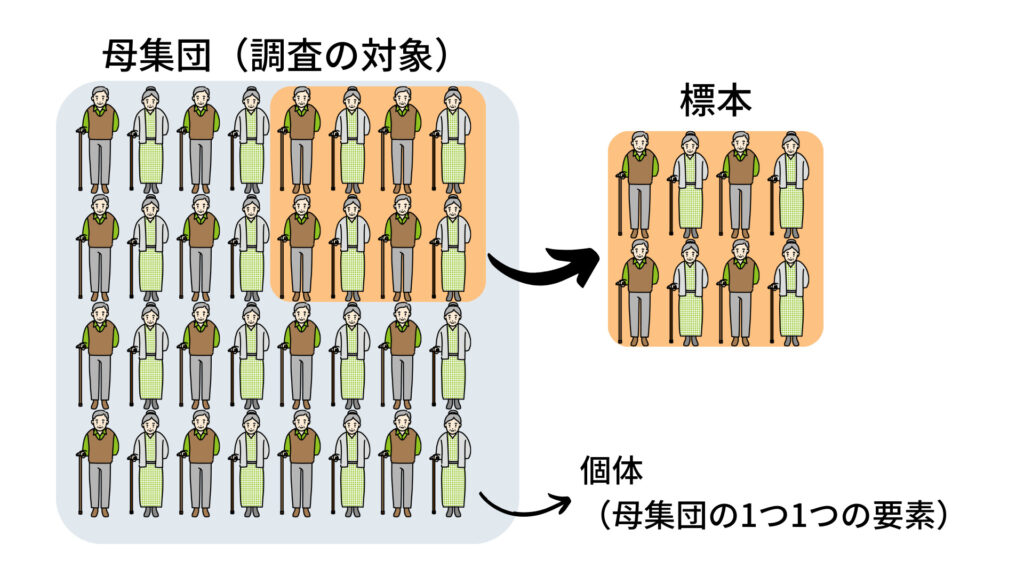
母集団。つまり、調査に対象が明らかになっていないと調査の結果(論文)をどのような患者さんに適応していいのかが分からないので誤った判断をしてしまう可能性があります。
この記事で統計とは「データの背景にある現象の法則性を知るための学問」です。ではどのようにデータの背景にある現象の法則性を知るかというと、
事実を観測することです!
結構大事なので大きめに書きました。統計学の目的の1つである「母集団の法則性を知る」ためには母集団全体を良く調べることが一番の方法となります。
具体的に言うと調査の対象となる人や物の集合の1人1人をすべて調べる方法が一番正確性の高い方法となります。
この方法を用いているのが国勢調査です。全体のデータを可能な限り手元に得て、全体の法則性や傾向を調べます。調査対象である集まり全てデータを調べることを全数調査といい、記述統計というデータの特徴をわかりやすくするための統計的手法を使用します。
しかし、この全数調査のように調査となる集合に存在する1人1人をすべて調べることは現実的に困難であることが多いです。リハビリテーション分野でも想像してもらうと難しいことは明らかであると思います。
そのため、調査の対象となる集合からさまざまな抽出方法で抽出された人たち、つまり標本をよく調べて、全体を調べる方法が生まれました。例えると、鍋の中にあるスープを味見して鍋の中にあるスープ全体の味を知るようなものです。
このようにあるデータの一部から確率という数学理論を用いて、その標本の元となるデータ全体の特徴を推測することを統計的推測と言います。(標本サイズが大きいほど、統計的推測の尤もらしさが上がる)
このような手法が打ち立てられたのはここ一世紀ほどで近代統計学とも言われています。
簡単にまとめると、多くの場合で母集団は観測不可能なことが多いため、観測可能な標本から母集団を推定する方法が生まれたのです。
この記事を以下の図にまとめました。
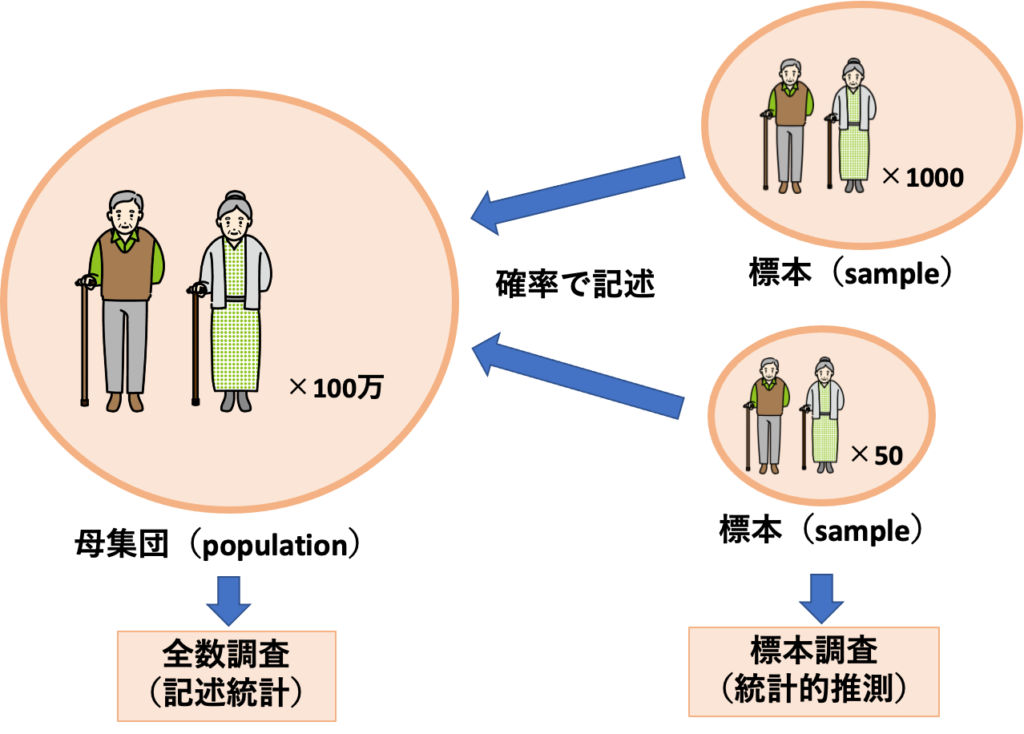
ご意見があればコメントよろしくお願いします。



