確率変数と確率分布

サバくん

確率だけではあまりにも抽象的かつ一般的であるため、具体的な事象を記述したり、分析したりするには不十分です。より簡単に確率を扱うために、確率変数と確率分布を使用しましょう。

確率変数

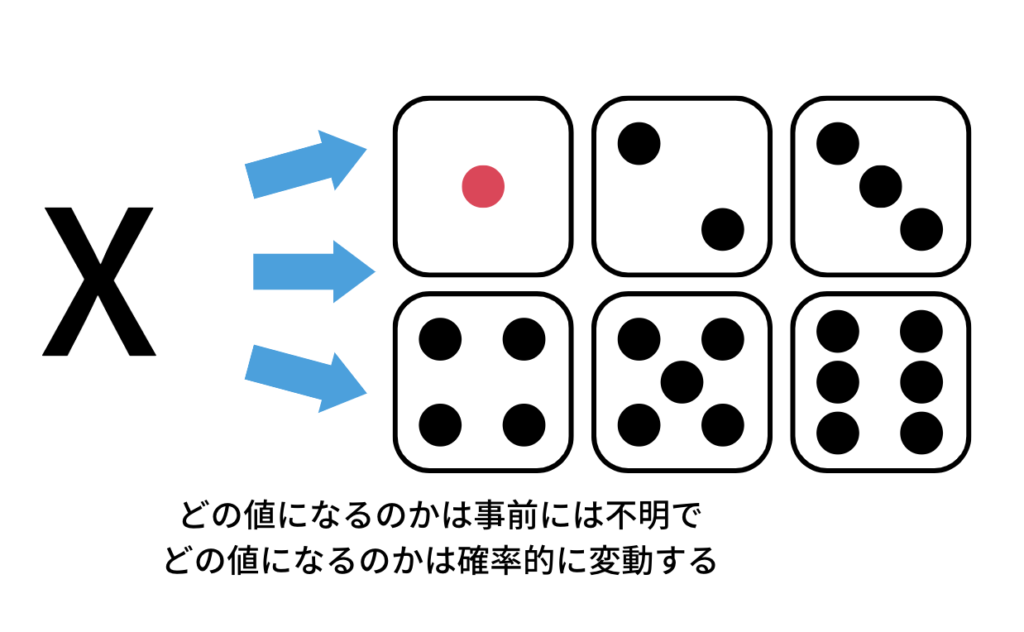
確率変数は様々な値をとりうる変数$X$があって、それぞれの値をとる確率が決まっているとき$X$を確率変数といいます。よく意味がわかりませんね、、

具体例で見てみましょう。わかりやすいのでサイコロを例に出します。（今回用意したサイコロは極めて精密に作られていて全ての目が同じ確率で出現するとします。）

サイコロの出る目は$1,2,3,4,5,6$なので、変数$X={1,2,3,4,5,6}$と置くと、

$$P(X=1) = 1/6, P(X=2) = 1/6, …., P(X=6) = 1/6$$

と表すことができます。このよう確率的に変動する変数、言い換えるとXの値は事前にわからないが取りうる値に確率が与えられている変数を確率変数と呼びます。イメージ的には変数とその変数の起こりやすさがセットになっている感じですかね。

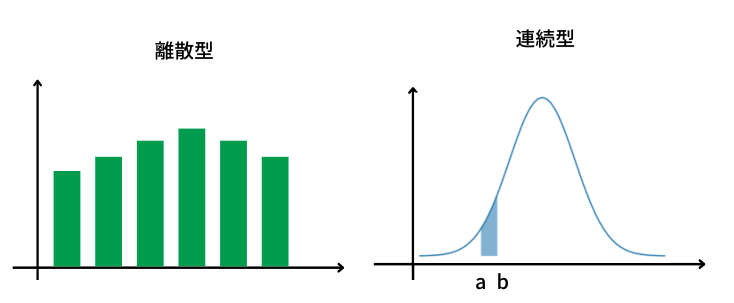
サイコロのように離散的な値をとる変数であれば、離散型の確率分布。連続的な変数であれば、連続型の確率分布といい区別されます。この2つの大きな違いはある値を一点で取るのか、値を範囲で取るのかの違いです。

少し数学的な説明になるので読み飛ばしてもらっても構いません、、

離散型の確率変数であれば、確率変数Xの取りうる値が$X={x_1,x_2, …, x_n}$としたときに確率変数とその起こりやすさを導出する関数（確率関数$f(x)$）の関係は

$$P(X=x_i)=f(x_i) (i=1,2,…,n)$$

と表現することができます。しかし、連続型の場合は確率変数を1点にしてしまうと起こりうる値が限りなく0に近い値となってしまいます。そのため範囲を指定してその起こりやすさを表現します。

$$P(a≦X≦b) = \int_{b}^{a}f(x)dx$$

このように範囲をとることで起こりやすさを表現することができます。このような関数は確率密度関数と呼ばれます。ちなみに、確率関数や確率密度関数は確率の公理を満たします。

少し数学的な説明だったので、わかりにくかった人もいると思います。次に記述する確率分布を見ると違いがわかりやすいと思います。

確率分布は先ほど説明した確率変数を表したものです（図や表で表すことが多い）。表で表す場合は横軸に確率変数、縦軸に確率変数の起こりやすさを表した分布です。離散型の場合は一つの値に対応する縦軸が起こりやすさを表しますが、連続型の場合は面積が起こりやすさを表しています。

確率変数の期待値$E$は確率変数がどのような値を取ることが「期待されるか」という意味で名付けられたもので、加重平均値と同じようなものです。

離散型の場合は

$$E(X)=\sum_{i}x_i f(x_i)=\mu$$

連続型の場合は

$$E(X)=\int_{-\infty}^{\infty} x f(x)dx=\mu$$

分散$V$は確率分布の散らばり具合の指標です。

離散型の場合は

$$V(X)≡E[(X-\mu)^2]=\sum_{i}(x_i- \mu) f(x_i)=\sigma^2$$

連続型の場合は

$$V(X)≡E[(X-\mu)^2]=\int_{-\infty}^{\infty} (x-\mu)^2 f(x)dx=\sigma^2$$

と表すことができます。