1次元のデータの可視化方法に箱ひげ図があります。箱ひげ図のいいところは外れ値がわかりやすいところです。
箱ひげ図を描画するのに必要なパーセンタイル（５要約数）について記述した後に箱ひげ図について記述します。
目次
パーセンタイルとはデータを小さい順から並べた時に一番小さい値から○（0〜100）％に位置する値のことを言います。
例えば1から100までの数字がデータとして得られた時に70％パーセンタイルは70になります。
具体的にみていきましょう。以下のような20個のデータが得られたとします。
15, 56, 49, 98, 9, 26, 24, 75, 42, 84, 2, 31, 35, 12, 55, 71, 68, 62, 83, 91
まず、これらを小さい値から大きい値になるように順番に並べます。
2, 9, 12, 15, 24, 26, 31, 35, 42, 49, 55, 56, 62, 68, 71, 75, 83, 84, 91, 98
例えば、この数列から40％パーセンタイルを得たい場合は
20個のデータ×40％＝20 なので小さい数から20個目に位置するデータは35となり、
このデータにおける40％パーセンタイルは35になります。
パーセンタイルの特別な場合をまとめたものを５要約数と言います。以下の表にまとめます。
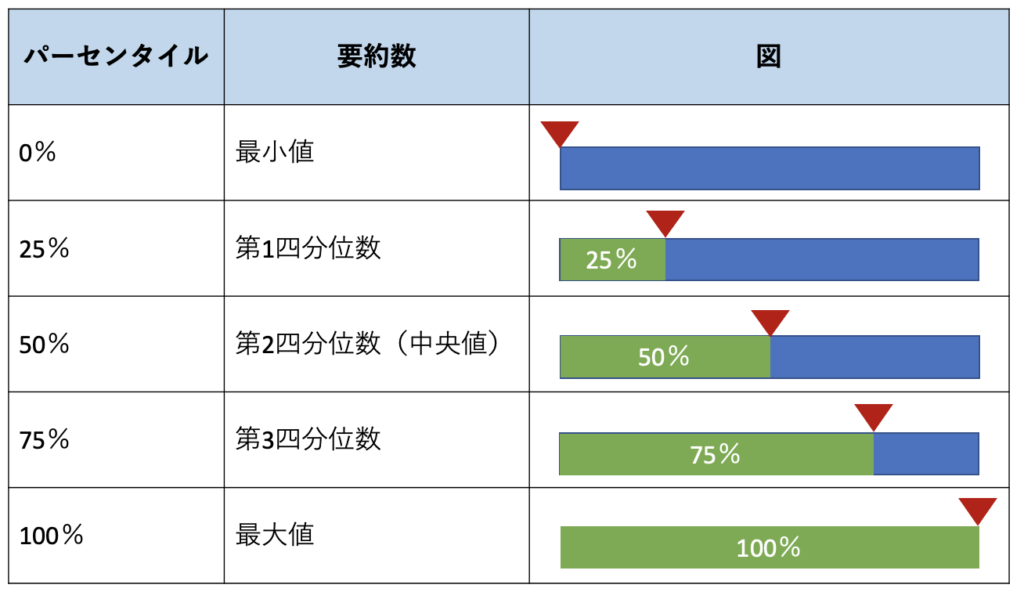
ちなみに 最大値ー最小値 （上の図で棒グラフの長さ）は範囲（レンジ）といい、ばらつきの指標になります。
第３四分位数ー第１四分位数 は四分位範囲と言います。この後箱ひげ図を描画するときに使います。
第５要約数を図にしたものが箱ひげ図（Boxplot）です。
データの中で極端い大きな値や小さな値をとる数を外れ値と言います。この外れ値が「人間の入力ミス」「計測機器の故障」などによる間違いによるものであれば、修正をしなければならいことがあります。
また、間違いではなくとも平均などの統計要約量に大きな影響を与えるため、修正をすることがあります。
一般的に
・第1四分位数ー1.5×四分位範囲より小さい値
・第3四分位数+1.5×四分位範囲より大きい値
を外れ値とすることが多いです。
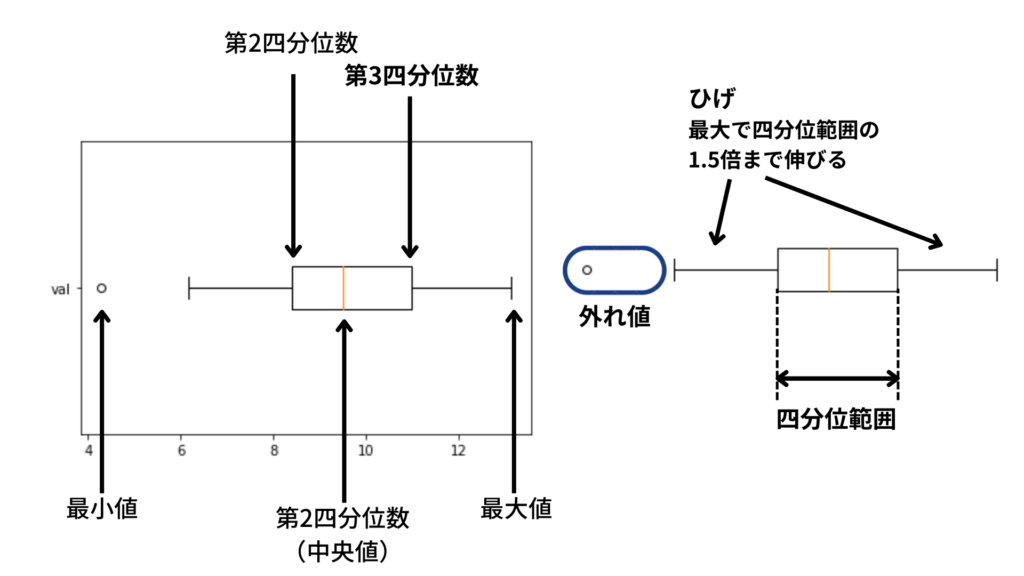
箱ひげ図を見るとデータの分布が
・中央によっているのか？まばらなのか？などの分布のばらつき
・大きい値に偏っているのか？小さい値に偏っているのか？などの分布の歪み
・分布から大きく外れている外れ値
を一目で確認することができます。
pytonで記述したい場合は以下の記事に書いています
箱ひげ図を描画する（python）
