統計学と確率

サバくん

手元にあるデータ（標本）からデータの元となっている母集団を推定する時には確率の考え方が大事になってきます。

ランダム性と確率

先に述べたように統計学では手元にあるデータ（標本）からデータの元となっている母集団を推定する時には確率（probability）の考え方が大事になってきます。

というもの、起こりうる結果がどういう要素を含んでいることはわかりますが、1回ごとの結果は偶然に左右されて事前に予測することは困難です。

例を挙げると、

といったようにこういった偶然に左右される不確実でランダムな問題と戦わなければならない。統計学においてこのランダム性と戦うツールが確率なのです。

確率の用語

苦手な人も多いとは思いますが、確率を扱っていくので確率の分野で扱われる用語について整理していきましょう。

試行（trial）

1回ずつの個別の結果が偶然に左右される観測を試行（trial）といいます。試行によって起こりうる結果を標本点（sample point）といいその全体の集合を標本空間（sample space）といいます。標本空間（sample space）は記号ではΩで表されます。

例えば、一般的なサイコロで表すと

サイコロの取りうる値は１から６の自然数なので標本空間

$$Ω={1,2,3,4,5,6}$$

となります。

サイコロのように取りうる値が限られている場合は標本点は有限個からなりますが、歩幅などの長さ、関節角度などの角度などのある区間内全てが取りうる場合は標本点は無限個となります。

$$Ω= (0, ∞)$$

事象（event）

事象とは標本空間の部分集合として定義されます。

例えば、標本空間が Ω={0,1} の標本空間の事象は

$${0,1}, {1}, {0}, φ$$

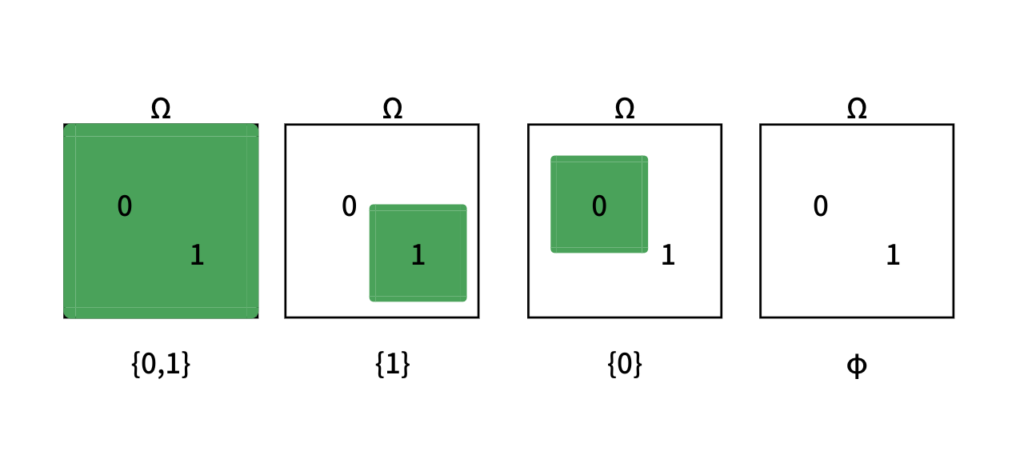
となります。（φはから集合のことで何も起こらないという意味で、空集合といいます。）

他にも事象に関する用語には根元事象、和事象、積事象、余事象、排反などがあります。

根元事象

試行によって起こりうる全ての結果のこと。例えばサイコロであれば$1,2,3,4,5,6$のことです。

和事象

複数の事象$A_1∪A_2∪･･･∪A_n$があったときに少なくとも1つの事象が起こる起こる事象のことです。

$$A_1∪A_2∪･･･$$

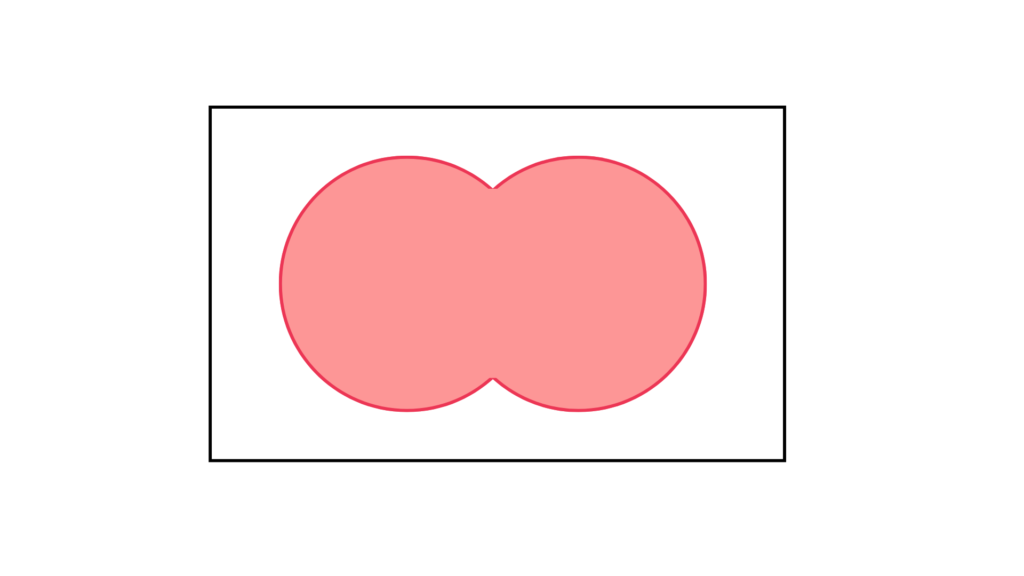
サイコロで例えると「3以上の事象」と「偶数の事象」の和事象は$2,3,4,5,6$となります。

積事象

複数の事象$A_1∪A_2∪･･･∪A_n$があったときに、複数の事象が同時に起こる事象のことです。

$$A_1∩A_2∩･･･$$

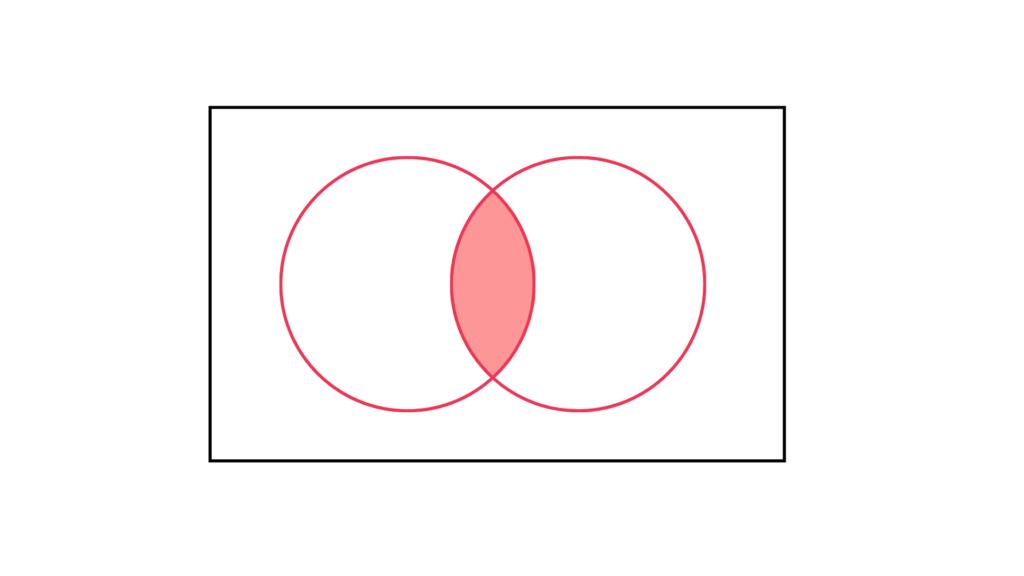
サイコロで例えると「3以上の事象」と「偶数の事象」の積事象は$4,6$となります。

余事象

ある事象$A$があったときに事象$A$が起こらない根元事象からなる事象のことです。

サイコロで例えると「偶数の事象」の余事象は $1,3,5$となります。

排反

2つかそれ以上の事象の積事象が空事象である時は互いに排反であると表現します。

サイコロで例えると「偶数の事象」と「奇数の事象」は互いに排反です。

確率

確率を数学的に表現すると

の3つの性質（確率の公理 or コルモゴロフの公理）を満たす関数のことを指します。この3つの性質を言い換えると確率は0以上1以下であり、各事象の積集合が空事象であれば（重なりがなければ）、和事象を満たす確率はそれぞれの事象の確率に等しいということです。

また、確率の定義は様々ありますが、代表的なものに

があります。

古典的確率

古典的確率は同様に確からしい（equally likely）を仮定した確率の定義の仕方です。つまり、根元事象それぞれ全て同様の確率で起こると仮定している確率のことです。中学校で学んだ人が多いのではないでしょうか？

サイコロを例に挙げるとサイコロの根元事象は6つあるのでそれぞれの目が出る確率は$1/6$となります。

頻度に基づく定義

頻度に基づく確率は大数の法則という重要な性質の基づいて考えられた確率です。つまり、ある試行を十分に大きい回数繰り返し行い、その相対度数を確率と定義する方法です。

例えば、サイコロを振って1の目が出る確率を知りたいときに、1000回振って1の目が出てきた回数を601回とすると

サイコロを振って1の目が出る確率は$601/1000≒6/10$となります。頻度という過去の情報に基づいて確率を定義していますね！

まとめ

今回は統計学と確率の記事を簡単に記載しました。分かりにくいところがあれば教えてほしいです

脱・統計学苦手療法士ロードマップ