サバくん
MediaPipeやOpenPoseなどのライブラリで座標が得られたけど、そこから角度を知りたいことは多いと思います。
角度の算出方法はいくつかあります。有名なものに「逆三角関数」や「偏角」を使ったものあります。
目次
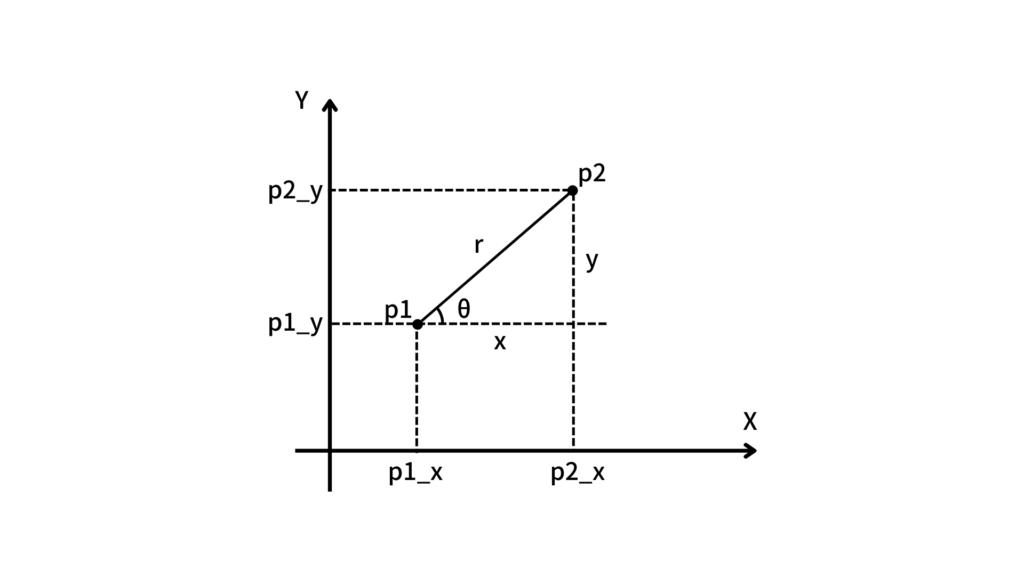
これから角度を求めていきますが、上の図のような2次元直交座標系で
2点（p1とp2）を通る直線と点p1を通るx軸と並行な線とのなす角を求めていくことを考えていきます。
import numpy as np
p1_x=1
p1_y=1
p2_x=2
p2_y=2
x = p2_x-p1_x
y = p2_y-p1_y
r = np.sqrt(pow(x,2)+pow(y,2))逆三角関数という三角関数の逆関数を用いることで座標から角度を求めることができます。
np.arc〇〇
np.arc〇〇で出力される数値の単位はrad(radian)です。そのまま扱ってもいいですが、np.degrees()で度に変換するとわかりやすいです。
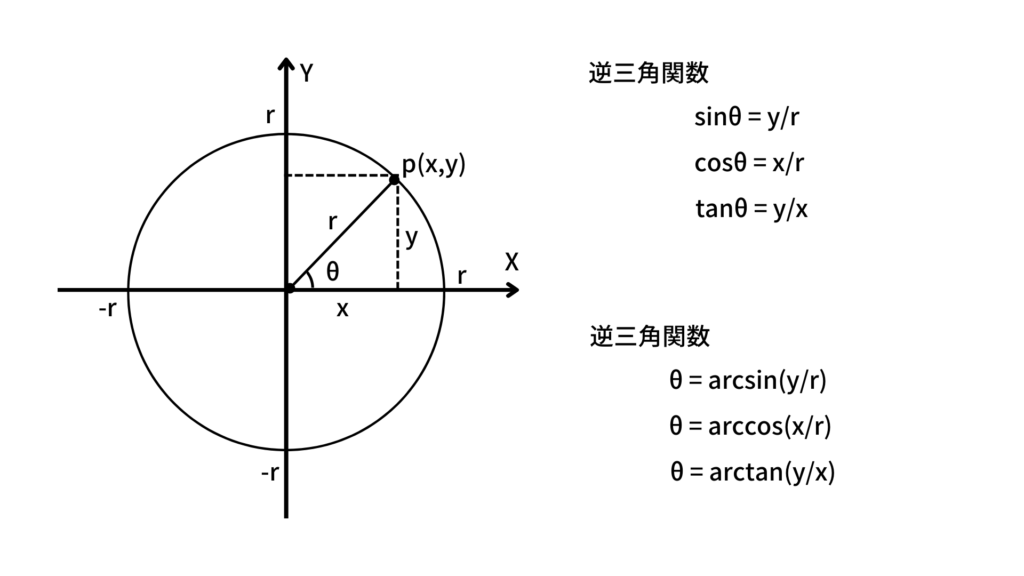
arcsin
rad=np.arcsin(y/r)
deg=np.degrees(rad)
print(deg)arccos
rad=np.arccos(x/r)
deg=np.degrees(rad)
print(deg)arctan
rad=np.arctan(y/x)
deg=np.degrees(rad)
print(deg)定義域と主値
逆三角関数にはそれぞれ定義域と値域があります。
定義域：引数の取り得る範囲（下の表でxの取り得る範囲）
主値：関数の出力が取り得る範囲（下の表でθの取り得る範囲）
| 逆三角関数 | 定義域 | 主値 |
| θ=arcsin(x) | −1≤x≤1 | −π/2≤θ≤π/2 |
| θ=arcsin(x) | −1≤x≤1 | 0≤θ≤π |
| θ=arctan(x) | −∞<x<∞ | −π/2≤θ≤π/2 |
定義域や主値の範囲を考えて適切な逆三角関数を選択する必要があります。
2点直交座標系を複素平面と考えると、偏角で角度を求めることもできます。
rad = np.angle(complex(x,y))
deg = np.degrees(rad)
if deg<0:
deg += 360
print(deg)ウィジットを使ってきちんと角度が算出できているのかを確認してみましょう。
def point2angle(p1_x,p1_y,p2_x,p2_y):
p1=(p1_x,p1_y)
p2=(p2_x,p2_y)
x=p2[0]-p1[0]
y=p2[1]-p1[1]
# Angle calculation
rad = np.angle(complex(x,y))
deg = np.degrees(rad)
if deg<0:
deg += 360
# 可視化のための準備
r0=25
def circle_y(x,r0,p):
a=p[0]
b=p[1]
r = np.sqrt(pow(r0,2)-pow(x-a,2))
return b+r, b-r
def line_y(x,p1,p2):
if p1[0]-p2[0] != 0:
a=(p1[1]-p2[1])/(p1[0]-p2[0])
b=(p1[0]*p2[1]-p1[1]*p2[0])/(p1[0]-p2[0])
else:
a=0
b=p1[1]
return a*x+b
x0=np.cos(rad)*r0
x_0=np.round(np.arange(x0+p1[0],r0+p1[0]+10e-100,.001),4)
x_1=np.round(np.arange(p1[0]-r0,x0+p1[0]+10e-100,.001),4)
# 可視化
c="gray"
plt.figure(figsize=(10,10))
plt.title("Angle")
plt.plot([p1[0],p2[0]],[p1[1],p2[1]],"*-")
plt.plot([p1[0],100],[p1[1],p1[1]],"black")
plt.plot(x_0,circle_y(x_0,r0,p1)[0],color=c)
if deg>=180:
plt.plot(x_1,circle_y(x_1,r0,p1)[0],color=c)
plt.plot(x_1,circle_y(x_1,r0,p1)[1],color=c)
plt.text(-90,80,f"{np.round(deg,2)}",fontsize=20)
plt.text(p1[0],p1[1],"p1",fontsize=15)
plt.text(p2[0],p2[1],"p2",fontsize=15)
plt.xlim(-100,100)
plt.ylim(-100,100)
plt.grid()from ipywidgets import interact
interact(point2angle, p1_x=(-100,100,1),p1_y=(-100,100,1),p2_x=(-100,100,1),p2_y=(-100,100,1))出力結果がこちら。きちんと角度を出力できていますね
