目次
算術平均, 相加平均(arithmetric mean)
算術平均(もしくは相加平均)は観測値の総和を観測値の総数で割った値です。
数式を書くと以下のようになります。
$$\bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}$$
また算術平均は$\sum_i^n(x_i-\bar{x})=0$が成り立ちます。$x_i-\bar{x}$は偏差と言い各観測値が平均値からどの程度離れているかを表しています。
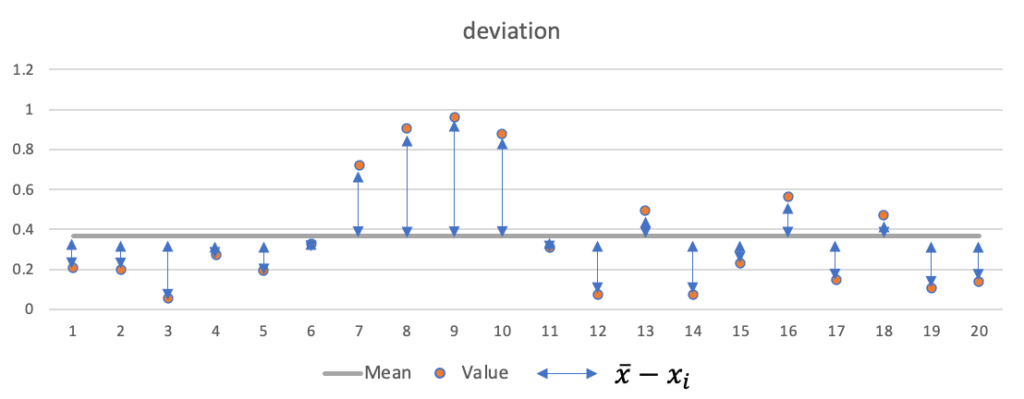
算術平均は全観測値の中心の位置の指標であり、観測値の重心を意味します。
幾何平均(geometric mean)
平均上昇率など、ある単位時間で平均してどの程度の上昇率があるかを調べたい場合は幾何平均を使用します。
$$x_G=\sqrt[n]{x_1・ x_2・\cdots・ x_n}$$
例えば、10m歩行を1週間ごとに計測し、それぞれ2.2倍, 1.7倍, 1.2倍, 1.1倍と変化していったとします。
その時は
$$\sqrt[4]{2.2・ 1.7・1.2・ 1.1} = 1.4906…$$
となり、4週間で平均して約1.5倍ずつ変化していったことがわかります。
調和平均(harmonic mean)
調和平均は観測値の逆数どうしの算術平均です。よく速さの平均を求める時によく使います。
$$x_H=\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n})$$
例えば、ある距離dを往復するとして、行きは時速4km、帰りは時速6kmで歩行したとします。
その時の平均時速は
$$x_H=\frac{1}{2}\frac{d}{(\frac{d}{4}+\frac{d}{6})} = 4.8$$
となり、平均時速は時速4.8kmとなります。
範囲や四分位範囲は2,4つの観測地のみを用いてばらつきを表現していましたが、全ての観測値を用いてばらつきを表現しているのが分散、標準偏差、変動係数です。
分散
ばらつきを表現するには平均から観測値がどの程度ばらついているのかを表現する必要があります。
ばらつきを表現するために偏差を使いたいですが、先に述べたように偏差の合計は0になるためばらつき具合を表現できません。そのため、偏差を2乗して総和したものを観測値の総数で割ります。
$$s^2=\frac{1}{n}\lbrace(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2\rbrace$$
こうすることによって平均まわりに観測値がどの程度ばらついているのかを表現することができます。
標準偏差
分散は偏差を2乗しているのでばらつきも2乗されています。そのため、観測値と分散の単位が異なっており、感覚的にばらつき具合が分かりずらいです。そのため、分散の平方根を取った値が使われます。この値を標準偏差と言います。
$$s=\sqrt{s^2}$$
変動係数
分布の中心が著しく異なるような場合には分散や標準偏差を使ってばらつき具合を比較することはできません。この時に使われるのが変動係数です。変動係数は標準偏差を平均値で割ることで算出することができます。
$$C.V.=\frac{s}{\bar{x}}$$




