度数分布とヒストグラム

さばくん

1次元のデータの分布を確認するときには度数分布を用いると簡単に把握することができます。

pythonを用いてヒストグラムを描画する方法も他の記事に書いているので参考にしてください。

度数分布表

度数分布表とは観測値の取りうる値をいくつかの階級（値の範囲）に分けて、その階級内に観測値がいくつあるのか（度数）を表にしたものです。

例えば、50人のMMSEを検査したときに

という値が得られたとします。この値を５区切りの階級ごとに観測値がいくつあるのか、つまり度数を数えて表にすると、以下の表になります。ちなみにその階級を代表する値のことを階級値と言います。普通は階級の下限値と上限値の中間の値を取ります。

表を見ると大体一様に数値が分布していることが読み取れます。数値の羅列では分かりにくかった分布を簡単に把握できます。

ヒストグラム

上のような度数分布でも分かりにくいという人はグラフで可視化してみましょう。

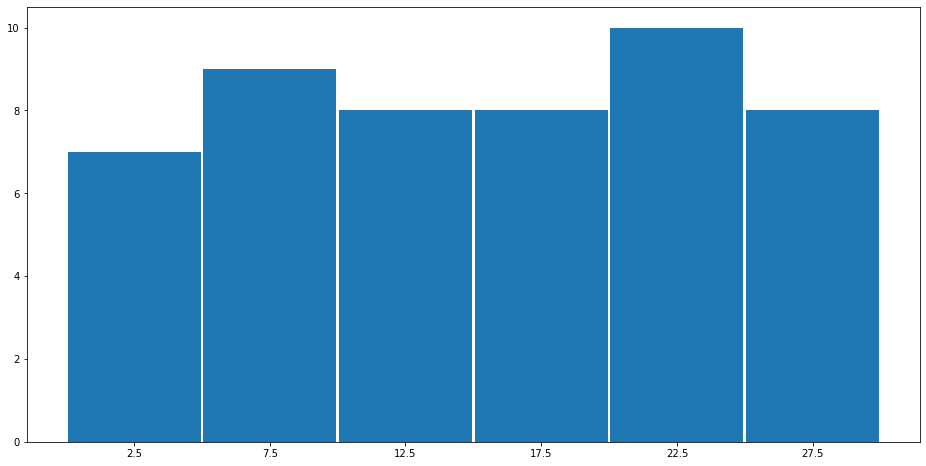
度数分布表を可視化したグラフがヒストグラムです。ヒストグラムは横軸に階級を縦軸に度数をとったグラフです。

実際に描画したものがこれです。（離散値なのでグラフに間隔を空けている。連続値の場合は間隔を空けない）

区切る階級によって

ヒストグラムは区切る階級の幅で印象がガラリと変わります。上のヒストグラムは階級幅を2にしたものです。

一様に並んでいるというよりは3つの山があるような印象を受けますね、

※一様分布から無作為に標本抽出してるので、一様分布に近い方が理想

どのような階級をとるのかについてルールはありませんが、スタージェスの公式を使い階級幅を決めることもあります。

スタージェスの公式 k≒1+log_2 n

追記：

統計に関する書籍にの度数分布の記事を読んでるとよく出てくるものに「相対度数」があります。

相対度数は全体の大きさを１とした時の各階級に属する観測値の割合のことです。

ちなみに累積度数、累積相対度数その名の通りその階級までの累積値です。

脱・統計学苦手療法士ロードマップ